Казимир Айдукевич / Язык и смысл

Казимир Айдукевич

Язык и смысл[1]

§ 1. Цель исследования

В настоящей работе я намерен выяснить некоторые семасиологические понятия, которые, как мне кажется, весьма важны для методологии наук и теории познания. Среди прочего я предложу дефиницию смысла выражений. Понятие “смысл”, которое я здесь имею в виду, — это не понятие субъективного смысла, появляющееся в некоторых психических актах, результатом которых является понимание этого выражения некоторым индивидом. Говоря о “смысле выражения”, мы будем иметь в виду нечто интерсубъективное, что присуще какому-то звуку речи относительно языка, а не с точки зрения человеческой личности. Важность этого интерсубъективного понятия смысла выражений для методологии и теории познания следует хотя бы из того, что утверждения наук являются ничем иным, как смыслом определенных предложений, присущих этим предложениям в определенном языке, а познание (в отличие от познавания), по крайней мере в своем наиболее совершенном виде, это как раз и есть смысл некоторых предложений, а возможно, и иных выражений.

Несмотря на значимость, каковой обладает понятие смысла в теории познания, это понятие нигде более, насколько я знаю, точно не было определено; большей частью довольствовались обращением к некоторому “усмотрению”, некоторой “интуиции” того, что понимается под смыслом. На нашем пути к дефиниции “смысла” мы будем продвигаться отчасти аналитически, отчасти синтетически и безапелляционно. В частности, мы будем стараться, чтобы наша дефиниция “смысла” как можно более долго оставалась в согласии с обыденным пониманием этого термина. Однако это будет возможно только до некоторой степени, поскольку мы стремимся к дефиниции, которая должна очертить понятие точное и четкое. Но объем привычного понятия “смысл” не является четко очерченным. Поэтому, стремясь четко обрисовать это понятие, мы вынуждены позволить себе некоторую свободу, четко очерчивая границы его объема в размазанном контуре обычного понятия. Эту границу можно провести так или иначе, причем вследствие нечеткости обычного понятия каждый выбор будет равноправен. Однако не каждый выбор будет обладать одинаковой ценностью с точки зрения его применения, т. е. с точки зрения результатов, которые можно было бы с его помощью получить.

Предлагаемая нами дефиниция “смысла” является именно такой дефиницией, которая влечет за собой далеко идущие последствия, ибо она в теории познания ведет к позиции, которую мы определяем как радикальный конвенционализм. Этим следствиям результатов настоящей работы мы посвятим отдельную статью, которая в ближайшее время должна появиться в журнале “Erkenntnis” с названием “Картина мира и понятийный аппарат” [Das Weltbild und die Begriffsapparatur][2].

Поскольку настоящая статья должна подготовить почву для ее эпистемологических последствий, то прежде всего обратим внимание на некоторые различия в процессах познания, особенно в процессах суждения.

§ 2. Суждение и его виды

Мы различаем суждения в логическом и психологическом отношении. В психологическом отношении суждениями являются некоторые психические явления, о характеристике которых много писалось и говорилось. Мы не намерены участвовать в этом споре, но только хотим обратить внимание читателя на определенные виды процессов суждения, отказываясь приводить точные дефиниции этих видов. Удовлетворимся их упоминанием.

Существуют процессы суждения (назовем так суждения как психические явления, в отличие от суждений в логическом смысле, которые в дальнейшем будем называть кратко суждениями), которые можно адекватно выразить предложениями некоторого языка. Такие процессы суждения назовем артикулированными процессами суждения. В оппозиции к ним существуют такие процессы суждения, которых нельзя выразить адекватно при помощи предложений; назовем их неартикулированными процессами суждения. Рассмотрим пример, который послужит нам иллюстрацией неартикулированного процесса суждения: в тот момент, когда я сижу за столом и пишу эти слова, в комнату входит служитель и вручает мне письма. Замечаю это, не прерывая работы. Это наблюдение состоит из различных переживаний [verschiedene Erlebnisse], в частности, из определенных процессов суждения. Стремясь придать им словесное выражение, я замечаю, что какие бы для этой цели не были выбраны слова, я адекватно не выражу ими процессов суждения, которые произошли во мне. Эти процессы имели достаточно туманный вид, тогда как процесс суждения, выраженный однажды в словах, обладает много более четкими чертами. Попробуем наш процесс суждения облечь в слова. Это можно было бы сделать при помощи следующих предложений: “служитель входит в комнату”, “Евгений входит в комнату”, “Евгений открывает дверь”, “Евгений пришел”, “Он пришел” и т. д. Каждое из этих предложений пригодно для адекватного выражения отличного от других процесса суждения, поскольку все процессы суждения, адекватно выраженные этими предложениями, отличаются между собой с точки зрения своего содержания. Но то, что я помыслил, увидев входящего служителя, в равной степени удается достаточно хорошо выразить при помощи каждого из этих предложений, из чего следует вывод, что каждым из этих предложений оно выражено не совсем точно. Это так, как если бы мы хотели провести в солнечном спектре линию, отграничивающую красный цвет от оранжевого. Можно пытаться это сделать по-разному. Каждая такая попытка одинаково удачна, но поскольку она отличается от прочих попыток, то она в той же мере неудачна, как и каждая иная.

В повседневной жизни с такими процессами суждения мы сталкиваемся на каждом шаге. Переходя через улицу и замечая приближающийся автомобиль, я высказываю суждение, но кажется, ни одно из предложений языка точно не соответствует моему суждению. Подобное происходит и тогда, когда мы вспоминаем о деле, которое следует исполнить. Так случается тогда, когда при решении научной проблемы приходят первые идеи. Общеизвестно, сколько нужно положить труда, прежде чем первая, сразу не поддающаяся выражению идея настолько прояснится в мыслях, что ее можно будет облечь в слова.

Не будем здесь дискутировать о том, заслуживают ли психические процессы, подведенные под название неартикулированных процессов суждения того, чтобы вообще называться процессами суждения. Достаточно, что мы обратили на них внимание. Для наших рассуждений важно отметить, что в дальнейшем мы будем принимать во внимание единственно процессы артикулированные.

В артикулированном суждении часто (если не всегда) происходит тихое либо громкое произнесение (или же чтение, записывание, слышание и т. д.). Это значит, что артикулированное суждение является сложным психическим процессом, в котором чаще всего можно более или менее фрагментарно выделить наглядное представление словесного образования. Это представление путается с иными составляющими, еще не поддающимися выделению в целостное артикулированное суждение. По нашему мнению, было бы ошибкой охарактеризовать этот процесс так, будто бы в этих случаях суждение следовало бы наглядному представлению предложения только в силу ассоциативности. Это представление сливается с процессом суждения в одно переживание и составляет, как это убедительно показал Гуссерль[3], его существенную составную часть.

Артикулированное суждение, существенной составной частью которого является наглядное представление предложения, назовем вербальным суждением. Вопрос о том, существует ли вообще артикулированное и невербальное суждение, мы оставляем в стороне. Научное суждение в стадии зрелости всегда совершается в вербальном мышлении. Среди тех составляющих процесса вербального суждения, которые превышают само воображение предложения, следует выделить момент убеждения, т. е. момент асерции. Он может быть позитивным или негативным в зависимости от того, состоит ли суждение в признании или отбрасывании, причем момент асерции может иметь различные градации интенсивности. Когда момент асерции совершенно отсутствует, то мы имеем дело с тем, что Мейнонг называет “Annahme”. Процесс суждения с позитивным моментом асерции мы называем позитивным убеждением, тогда как процесс суждения с негативным моментом асерции — негативным убеждением.

В дальнейших выводах мы будем пользоваться оборотами “X признает предложение Z”, а также “X отбрасывает предложение Z”. Первый из этих оборотов означает, что “X при помощи Z выражает позитивное убеждение”. При этом необязательно X должен высказывать или писать предложение Z, но он может также слышать это предложение или читать, наконец он вообще не обязан воспринимать его чувствами, а может его себе только воображать. Тогда X переживает всегда словесный процесс суждения с положительной асерцией, составляющей воображения которого является представление предложения Z.

“X отбрасывает предложение Z” это не то же самое, что “X признает отрицание предложения Z”. Отрицание является иным видом асерции, чем признание. Различие между отбрасыванием предложения Z и признанием предложения Z состоит не в том, относительно чего (т. е. относительно предложения Z или относительно его отрицания) мы занимаем одну и ту же (а именно, позитивную) позицию утверждения. Различие между признанием предложения Z и отрицанием предложения Z состоит в том, что относительно одного и того же предложения мы один раз занимаем позитивную позицию, а другой — негативную.

“X отбрасывает предложение Z” значит: “X занимает негативную позицию относительно того предложения, которым бы он воспользовался для выражения признания предложения Z,”. Отрицательное убеждение, заключающееся в отбрасывании предложения, и положительное убеждение, заключающееся в признании этого же предложения называются противоположными убеждениями. Приведенное выше пояснение необходимо еще дополнить следующим замечанием. Когда мы говорим, что X признает предложение “падает снег”, то мы не имеем в виду того, что X выражает такое суждение, какое обычно выражает немецким предложением “падает снег”. Говоря, что X признает предложение “падает снег”, мы не задумываемся над тем, пользуется ли X этим предложением так, как это ему предписывает делать русский язык, или же иначе. Таким образом, когда мы здесь говорим, что X признает предложение “падает снег”, то из этого не следует, что X верит в то, что со словесным звучанием этого предложения X связывает некоторое положительное убеждение. Возможно, это убеждение, зависит от того, каким образом его вербальный состав определяется русским языком; возможно также, что это соответствие иного вида.

В школе Брентано используются предложения формы “X признает Y”, понимаемые как утверждение, что Y является тем предметом, в существование которого верит X. Наши вышеприведенные объяснения относительно этого оборота выразительно показали, что мы им пользуемся в совершенно ином смысле, на что еще раз со всей силой обращаем внимание. И это все, что можно сказать о суждении как психическом процессе.

Обратимся сейчас к суждению в логическом отношении [logischer Hinsicht]. Под суждением в логическом отношении мы понимаем смысл [Sinn], который соответствует предложению в некотором языке. Если мы имеем дело с артикулированным процессом суждения, который удается выразить в предложении Z языка S, тогда назовем смысл, которым это предложение обладает в этом языке, также содержанием [Inhalt] этого процесса суждения. (Здесь не стоит вопрос, можно ли неартикулированным суждениям также приписывать нечто такое, как содержание.) Суждение (в логическом смысле) может быть утвердительным либо отрицательным, однако оно не может быть признающим или отбрасывающим, поскольку моменты асерции содержаться только в психологическом процессе суждения, но не в его содержании.

§ 3. Соответствие смыслов как необходимая характеристика языка

Язык однозначно характеризуется не только запасом слов и правилами своего синтаксиса, но также и способом, каким словам и выражениям соответствует их смысл. Если бы кто-нибудь пользовался словами русского языка, но связывал бы с ними иные смыслы, чем обычные, то мы определенно не посчитали бы этот язык русским языком, но разве что каким-то криптоязыком.

Таким образом, к характеристике однозначности языка относится соответствие между его звуками (или же написанными знаками и т. п.) и их смыслом. Это соответствие назовем характерным для языка подчинением смыслов. Оно еще не произведено, если установлено соответствие слов или выражений языка и названных ими предметов, ибо, во-первых, не все выражения называют предметы, но среди них единственно те, которые имеют номинативный характер, т. е. имена, тогда как смыслом обладают все слова и выражения языка. Во-вторых, два выражения могут называть один и тот же предмет, однако обладать различными смыслами. Так, например, выражения “самая высокая вершина в Европе” и “самая высокая вершина в Швейцарии” называют один и тот же предмет, однако имеют различный смысл. Традиционная логика не занималась смыслом всех выражений, но в своих выводах ограничивалась смыслом имен, которые отождествляла с содержанием понятий, соответствующих этим именам. Тот же пример, послуживший выше выяснению различия между смыслом имени и предметом, который обозначен этим именем, может служить в традиционной логике указанием на различия между содержанием и объемом понятия (номинального). Содержание понятия [Begriffsinhalt] и смысл [Sinn] имени являются хотя достаточно и близкими, но разными понятиями.

§ 4. Правила смысла

Если бы мы уже захотели здесь привести дефиницию термина “смысл выражения”, то зашли бы слишком далеко[4]. Короткие замечания, которые мы посвятили этому термину, предназначались лишь для устранения наиболее разительных недоразумений.

В этом параграфе мы намерены привести основополагающий для дальнейшего изложения настоящих рассуждений тезис, который временно и еще не совсем точно можно сформулировать следующим образом: смысл, которым обладают выражения языка, в определенной степени определяет правила употребления этих выражений. Позже этому тезису мы придадим точную формулировку, сейчас же объясним его и обоснуем.

Смысл, который кто-либо связывает с некоторым выражением, зависит от типа мысли, который этим выражением представляется, или обычно представляется. Смысл, которым наделено выражение, определяет, таким образом, соответствие между этим выражением и некоторого типа мыслями. Конечно, все те, кто пользуется одним и тем же выражением в одном и том же смысле, не обязаны нумерически связывать с ним одну и ту же мысль (понимаемую как психически реальный, индивидуальный процесс). Естественно, это было бы невозможно у различных личностей, а также и у одной личности, пользующейся одним и тем же выражением в разное время. Мы лишь утверждаем, что если они должны всегда пользоваться одним и тем же выражением в одном и том же смысле, то они должны всякий раз связывать с этим выражением мысли, принадлежащие к типу, однозначно очерченному смыслом этого выражения.

Здесь мы не будем пытаться очертить позицию, позволяющую выделить типы мыслей, которые ставятся в соответствие выражениям посредством их значений. Вместо этого мы подробнее займемся последовательностью шагов, служащей обнаружению недоразумений. Речь здесь идет о шагах, служащих обнаружению того [обстоятельства], что кто-то связывает с некоторым выражением, например, с каким-то предложением смысл, отличный от нашего. Рассмотрим сначала пример такой последовательности шагов.

Допустим, что не совсем деликатно коснулись чьего-то обнаженного и еще чувствительного зубного нерва. Этот кто-то вздрогнул и издал крик. Без сомнения, в этой ситуации было бы излишним спрашивать, почувствовал ли он боль. Однако представим, что такой вопрос поставлен и пациент ответил на этот вопрос отбрасыванием [Verwerfung] предложения “болит”. Как следует оценить это поведение? Во-первых, можно допустить, что пациент врал, т. е. в действительности он не отрицал предложение “болит”, а лишь делал вид, что отрицает это предложение. Во-вторых, существует возможность, что пациент не врал и действительно отрицал предложение, но вместе с тем не почувствовал никакой боли. Наконец, существует также возможность, что пациент не врал, а значит отрицал предложение “болит” и действительно почувствовал боль, но с этим предложением связывал иной смысл, чем мы. Во всяком случае мы исключаем такую возможность, чтобы кто-нибудь, чувствуя боль и отрицая при этом предложение “болит”, связывал с этим предложением тот же смысл, что и мы. В тот момент, когда мы убедились, что кто-то, почувствовав боль, отрицает предложение “болит”, то из этого можно сделать вывод, что он связывает с этим предложением иной смысл, нежели мы.

Тем самым мы отыскали последовательность шагов, служащую обнаружению недоразумений. Ее схему можно было бы сформулировать так: намереваясь решить, использует ли кто-нибудь определенное предложение в том же смысле, что и мы, находим для этого предложения некоторый выделенный тип переживаний тем отличающийся [от прочих], что переживаний этого типа нам достаточно для решительного принятия данного предложения. Обнаруживши, что интересующий нас индивид, несмотря на наличие переживания указанного типа, отбрасывает соответствующее предложение, мы отсюда делаем вывод, что он с этим предложением связывает иной смысл, чем мы. Отметим также, что этот вид переживаний, соответствующий данному предложению, является особо выделенным, а это выделение заключается не только в том, что наличие переживания этого вида совершенно достаточно ему для признания этого предложения; оно непосредственно должно приводить к признанию этого предложения, т. е. переход от переживания к признанию предложения не может быть разбит на несколько шагов. Если, например, признания некоторых посылок (это ведь тоже можно назвать переживанием) мне достаточно для принятия отдаленного заключения, а кто-то другой, признавая эти же посылки, все же отрицает предложение, в котором я выражаю заключение, то я не буду это считать доказательством существования недоразумения между нами относительно предложений — посылок или заключения, но смогу это для себя объяснить иначе. Какой выделенный тип переживаний в выше изложенном смысле соответствует данному предложению — это можно от случая к случаю обнаружить на основе языковой интуиции.

Выше описанные шаги давали бы бесспорные результаты, если бы их применение на практике всегда не было затруднено тем обстоятельством, что никогда совершенно уверенно нельзя утверждать, что в иной особе действительно наличествуют переживания соответствующего вида и действительно ли она отбрасывает соответствующее предложение, или же только создает видимость отбрасывания. Тем не менее утверждение, образующее основание этих шагов, а именно, что если кто-то испытывая переживание вида D отбрасывает предложение Z, то он с этим предложением связывает иной смысл, чем мы, это утверждение является аподиктически достоверным, если только этот вид переживаний оказался соответственно подобранным. Едва ли нужно говорить о том, что таким образом можно утверждать только существование недоразумения, но нельзя утверждать, что произошло понимание. Другими словами, приведенное выше описание последовательности шагов является лишь необходимым, но не достаточным критерием того, что кто-то с некоторым предложением связывает тот же смысл, что и я.

Рассмотрим еще и иной пример обнаружения недоразумений. Допустим, что некто равно признает как предложение “если А, то В”, так и антецедент “А” этого условного предложения, однако отбрасывает его консеквент “В”. Если он действительно так делает, а не только делает вид, то с целью выяснения такого поведения можно допустить, что в момент отрицания консеквента “В”, он уже успел забыть о том, что признавал посылки. Однако, если он помнит о них в момент отрицания консеквента “В”, то для нас это безошибочный признак того, что он пользуется, по крайней мере, одним из выражений “если А, то В”, “А”, “В” не в том же смысле, что мы. А именно, мы считаем невозможным, чтобы некто пользующийся выражениями русского языка в том же смысле, что и мы, признавал предложение вида “если А, то В” и его антецедент “А” и вместе с тем отрицал его консеквент “В”.

Рассмотрим внимательнее утверждения, на которые мы опирались в обоих приведенных выше примерах. Первое утверждение говорит, что одновременно невозможно испытывать с чувством боли негативное убеждение, заключающееся в отбрасывании по-русски правильно понимаемого предложения “болит”. Таким образом, это утверждение говорит о невозможности появления в сознании переживаний некоторого вида (чувства боли) одновременно с иным переживанием (отрицательным убеждением определенного вида). Обозначим через “H” тип мысли, соответствующий посредством его русского смысла предложению “если А, то В”, через “V” — тип мысли, соответствующий посредством его русского смысла антецеденту “А”, а через “N” — тип мысли, соответствующий посредством его русского смысла консеквенту “В”. Тогда второе утверждение может быть сформулировано следующим образом: одновременное переживание положительных убеждений вида H и V исключает возможность одновременного переживания отрицательного убеждения, противоположного мысли типа N.

В таком представлении утверждения, составляющие основу последовательности шагов, служащих обнаружению недоразумений, звучат так, как будто речь в них идет только о психологическо-эмпирических истинах. Однако, по нашему мнению, дело обстоит иначе, поскольку оба установленных выше утверждения не были заимствованы из опыта, но являются аналитическими. Им не угрожает опасность быть опровергнутыми в опыте, подобно тому, как это не грозит, например, предложению, что нагретая при нормальном давлении до 100°С вода кипит.

Общеутвердительное предложение вида “каждое А есть В” только тогда требует эмпирической проверки и только тогда оно может быть опровергнуто в опыте, если о некотором X можно утверждать, что оно есть А без обращения к тому, что X есть В, или каких- либо иных данных, из которых можно было бы вывести, что X есть В. Если вопрос, действительно ли X есть А, нельзя разрешить без предварительного утверждения (в приведенном выше смысле), что X есть В, то скажем, что свойство быть В является для понятия А конституционным [konstitutiv ist]. Предложение “все петухи поют” требует эмпирической проверки и может быть опровергнуто опытом. Предложение “каждый петух является птицей” не зависит от свидетельств опыта, ибо нельзя утверждать о некотором X, что он является петухом покамест остаются сомнения, является ли X птицей. Точно так же и предложение “нагретая до 100°С при нормальном давлении вода кипит” не является эмпирическим предложением и не может быть опровергнуто в опыте, поскольку свойство “кипеть при нормальном давлении” является конституционным для понятия воды, нагретой до 100°С.

Не так ли обстоит дело и с нашими выше приведенными двумя утверждениями? Рассмотрим утверждение: тот, кто правильно понимает [высказанное] по-немецки предложение “если А, то В”, тот не может отбросить консеквент “В”, если признает условное предложение “если А, то В” и его антецедент “А”. Разве можно с какой-то долей уверенности утверждать, что некто правильно понимает [высказанное] по-немецки предложение “если А, то В”, если еще не известно, сможет ли он отбросить консеквент, признавши условное предложение и его антецедент? Или разве можно утверждать, что некто связывает с предложением “болит” смысл, сопоставляемый ему в немецком языке, если еще нет уверенности в том, что он отбросит это предложение тогда, когда будет одновременно испытывать боль? По нашему мнению, это невозможно, а тем самым в обсужденных выше утверждениях приведены свойства, конституционные для понятия употребления этих предложений в соответствии с их смыслом. В этом месте мы еще не можем точно доказать это утверждение, поскольку наши рассуждения находятся в стадии неуточненных понятий, в которой еще невозможно ничего точно доказать. Однако мы убеждены в истинности нашего утверждения и склонны считать, что и читатель согласится с нами. Однако более не задерживаемся на этом.

Анализ шагов, служащих обнаружению недоразумений, нам показал, что существует связь между смыслами, соответствующими выражениям языка, и способом, каким этими выражениями мы пользуемся, связь, которую можно сформулировать, например, в следующих правилах: лишь тот связывает с выражениями русского языка подчиненный им в этом языке смысл, кто испытывая такого-то и такого вида чувства (например, чувство боли) готов признать некоторое предложение (например, болит). Анализ второго примера привел нас к следующему утверждению: только тот связывает с выражениями русского языка смысл, соответствующий им в этом языке, кто, признавая предложение вида “если А, то В”, а также “А”, готов признать также предложение “В”.

Как кажется, для каждого языка, в котором смысл его выражений однозначно очерчен, можно установить правила, сформулированные по следующей схеме: только тот со словами и выражениями языка S связывает смысл, сопоставленный им этим языком, кто в ситуациях типа L готов признать предложение типа Z (причем “Z” может оказаться функцией “L” или же составной частью “L”, как это имело место во втором примере). При этом “X готов в ситуации L признать предложение Z” означает не что иное как: “если X в ситуации L ответит на вопрос, представленный предложением Z со знаком вопроса, то он тем самым признает предложение Z”. Далее, поскольку ответ на вопрос, выраженный предложением Z со знаком вопроса может состоять только в признании или отбрасывании предложения Z, то можно вместо “X отвечает на вопрос, представленный предложением Z со знаком вопроса” сказать также “X признает предложение Z либо X отбрасывает предложение Z”. Таким образом, мы можем наше понимание этой готовности выяснить следующим: “X готов в ситуации L признать предложение Z” значит то же, что “если X находится в ситуации L и при этом или признает предложение Z, или отрицает его, то X признает предложение Z”. Последнее пояснение совершенно исключает из этой “его готовности” мифологическое понятие психической диспозиции.

Такого типа правила можно сформулировать для различных языков. Коротко назовем такие правила правилами смысла. Следовательно, правила смысла устанавливают соответствие определенных предложений ранее названным, особо выделенным типам данных, при переживании которых отбрасывание данного предложения может произойти единственно при попрании его смысла.

Однако не для всех языков можно сформулировать все правила смысла точно и несомненно. Повод приведем позже. Однако для искусственного языка символической логики эту задачу можно решить легко и полностью. Обычное исчисление предложений с первичными знаками Й“Й” и “~” обладает двумя так называемыми правилами вывода. Ими являются правило отделения, которое позволяет вывести “В” из “АЙВ” и “А”, а также правило подстановки. Кроме того, правилами вывода могут быть дефиниции (если их понимать как правила замены одних выражений другими). Все правила вывода можно легко преобразовать в правила смысла. Так, например, из правила отделения можно следующим образом образовать правило смысла для знака “Й”: “только тот со знаками языка логистики связывает смыслы, которые подчинены этим знакам посредством этого же языка, кто готов признать предложение “В”, если признает предложения вида “АЙВ” и “А”. Опять же, из дефиниции знака “v“, позволяющей подставлять “АvВ” вместо “~АЙВ” можно образовать следующее правило смысла: только тот связывает со знаками языка логистики смыслы, соответствующие этим знакам в языке логистики, кто готов признать каждое предложение S₁, возникающее из предложения S₂ вследствие замены выражения вида ~АЙВ” выражением “АvВ”, если он признает предложение S₂. Как для этого искусственного языка, так и для естественных языков можно было бы установить аналогичные правила смысла, хотя это предприятие встретилось бы с большими трудностями и его не удалось бы провести исчерпывающим образом.

Итак, смысл слов и выражений некоторого языка определяют обсужденные выше правила смысла, требующие от каждого, кто пользуется этим языком, определенных действий в отношении узнавания предложений этого языка в некоторых ситуациях. Кто не руководствуется этими правилами смысла, тот тем самым доказывает, что с выражениями, принадлежащими этому языку, он не связывает того смысла, который им в этом языке соответствует, а следовательно не пользуется этим языком, но каким-то другим, одинаково звучащим. Происходящие согласно этим правилам смысла действия, подобны действиям, соответствующим правилам фонетики или синтаксиса. Ими можно руководствоваться, хотя их и не нужно знать явным образом. О том, что правила смысла требуют признания данного предложения мы убеждаемся тогда, когда замечаем, что противное поведение, т. е. отбрасывание этого предложения вместо его признания должно быть понято как нарушение присущего данному языку соответствия смыслов. Происходящее согласно с правилами смысла признание предложений, отличается четкой очевидностью и неотвратимой решительностью[5].

§ 5. Дедуктивные, аксиоматические и эмпирические правила смысла

Сейчас мы перечислим некоторые виды правил смысла, встречаемые в существующих языках. Я намерен привести три вида правил, называя их 1) дедуктивными, 2) аксиоматическими, 3) эмпирическими, и не претендую на полноту перечисления.

Правило смысла, приведенное ранее по образцу правила отделения, представляет собой пример дедуктивного правила смысла. Ему можно было бы придать следующую формулировку: только тот связывает с выражением немецкого языка подчиненный ему в этом языке смысл, кто готов признать предложение “В”, если он признает предложение “если А, то В” и его антецедент “А”. Как уже выше упоминалось, можно рассмотреть другие примеры дедуктивных правил смысла, исходя из дефиниции. Например, если в языке арифметики “2” определена как “1 + 1”, то в этом языке обязательно правило: только тот связывает со знаками арифметики смысл, который им присущ в языке арифметики, кто готов признать предложение Z, содержащее знак “2”, если он признает предложение, отличающееся от Z только тем, что вместо “2” в нем находится знак “1 + 1”.

От всякого, кто хочет пользоваться выражениями данного языка в согласии с их смыслами, каждое дедуктивное правило смысла требует готовности определенным образом выводить следствия из некоторого вида посылок. Таким образом, дедуктивное правило смысла подчиняет каждому предложению некоторого типа как посылке предложение иного типа как заключение (либо же, если правило смысла требует готовности вывода из нескольких посылок, тогда оно ставит в соответствие каждому классу предложений определенных типов как посылкам определенный тип предложения как заключению).

Отсюда очевидно, что каждое дедуктивное правило смысла определяет отношение, членами которого являются предложения (или же классы предложений), но и это отношение взаимно однозначно соответствует этому правилу смысла. Область (Vorbereich), кообласть (Nachbereich) и поле (Feld) этого отношения назовем областью, кообластью и полем этого дедуктивного правила смысла. Однако объемом (Umfang) дедуктивного правила смысла назовем класс, элементом которого является упорядоченная пара предложений (или пара: класс предложений–предложение), тогда и только тогда, когда между первым и вторым членом этой пары имеет место отношение, определенное этим дедуктивным правилом смысла.

В языках аксиоматизированных систем несомненно существуют примеры того, что мы называем аксиоматическими правилами смысла. А именно, от каждого, кто хочет пользоваться выражениями такой системы со смыслом, поставленным им в соответствие языку этой системы, требуется безусловно, чтобы он был готов безоговорочно признать предложения, принятые в качестве аксиом. Однако я считаю, что такие аксиоматические правила смысла обязательны также для обычных естественных языков. Кажется, что от каждого, кто с выражениями, например, “всякий” и “есть” связывает смысл, соответствующий им в русском языке, требуется, чтобы он был готов безоговорочно признать любое предложение вида “всякое А есть А”. Как кажется, вообще все так называемые a priori очевидные предложения указывают на аксиоматическое правило смысла, которое каждому предписывает признать предложение этого вида, кто не намерен нарушать присущего языку соответствия смыслов. Подобно тому, как дедуктивным правилам смысла соответствует отношение между предложениями, так опять же, аксиоматическому правилу смысла соответствует класс тех предложений, которые согласно этому правилу следует признать. Этот класс предложений назовем областью этого аксиоматического правила смысла.

Третий класс образуют эмпирические правила смысла. Особенность этих правил такова, что в них приводится в виде ситуации, в которой согласно присущему в языке соответствию выражений их значениям требуется готовность признания предложения, такое переживание, которое является исключительным или среди прочего заключается в переживании некоторого впечатления. В соответствии с этим правилом, как кажется, поступают тогда, когда признают предложение “болит” при переживании зубной боли. Если бы мы о ком-нибудь узнали, что этот кто-то при сильном раздражении обнаженного чувствительного зубного нерва испытывает нормальное, с нашей точки зрения, чувство и несмотря на это не готов признать предложение “болит”, но отбрасывает это предложение и признает, например, предложение “испытываю приятное”, тогда мы усмотрели бы в его поведении, как уже было сказано, доказательство того, что он не связывает с предложениями “болит”, “испытываю приятное” тот же смысл, что и мы.

Существуют два вида эмпирических правил смысла, которые мы называем простыми и составными эмпирическими правилами смысла. Эмпирическое правило смысла является простым, если утверждает: только тот не нарушает присущего языку подчинения смыслов, кто ввиду переживания такого-то и такого впечатления готов признать так-то и так звучащее предложение. С другой стороны, составным эмпирическим правилом смысла назовем такое правило, которое требует готовности признать так-то и так звучащие предложения при выполнении некоторых условий, которые, среди прочего, состоят в переживании некоторого впечатления. Совокупность таких условий, как и отдельные впечатления, мы назовем эмпирическими данными (Erfahrungsdata). Они, например, могут состоять в наличии впечатлений и неартикулированных суждений, в которых ситуация признается “нормальной”. Возможно, что составные эмпирические правила смысла требуют признания некоторых предложений на основании ряда следующих друг за другом впечатлений и некоторых прочих данных. Как кажется, это имеет место для так называемых предложений, относящихся к внешнему миру. Если для обычных естественных языков не удается отыскать безупречных примеров эмпирических правил смысла, управляющих нашими высказываниями о так называемом внешнем мире (а эти правила определенно не являются простыми эмпирическими правилами), то причиной этого, как кажется, является то, что так называемые естественные языки не суть языки в точном значении этого слова, поскольку присущее им подчинение смыслов неустойчиво и изменчиво (см. последний параграф этой работы).

Выражения, к которым относятся (существенно) эмпирические правила смысла, назовем выражениями с эмпирическим смыслом и поделим их на выражения с простым и составным эмпирическим смыслом в зависимости от того, являются ли соответствующие эмпирические правила смысла все составными, или же среди них встречаются простые эмпирические правила смысла. Выражения, являющиеся именами внешних предметов и их свойств, кажется, должны иметь составной смысл, если вообще имеют какой-либо эмпирический смысл. Простым эмпирическим смыслом, как кажется, обладают только имена объектов, принадлежащих миру психики, и их свойства. Поскольку в естественных языках имена внешних предметов и имена свойств психических объектов часто звучат одинаково (так, например, говорится о “красной” розе и о содержании некоторого впечатления), то отсюда у не обращающих на это внимания теоретиков познания возникли различные трудности и парадоксы, которые их привели к отказу приписывать внешним предметам так называемые чувственные свойства. Но об этом лишь коротко; этим вопросом я намерен заняться подробнее в другой работе. Равно как аксиоматические, так и дедуктивные правила смысла совместно назовем дискурсивными правилами смысла. Языки, в которых обязательны только дискурсивные правила смысла (например, языки чистой логики и чистой математики), назовем дискурсивными языками. Языки, в которых обязательны эмпирические правила смысла, будем называть эмпирическими языками.

Как для дедуктивных правил смысла, которые связывают предложения (или же классы предложений) с предложениями, мы утверждаем, что каждому из этих правил соответствует отношение между предложениями, так и эмпирическим правилам смысла можно подчинить отношение между данными опыта и предложениями. Область этого отношения состоит из чувственных данных, кообласть — из предложений. Объемом эмпирического правила смысла назовем класс, элементом которого является пара <чувственные данные — предложение> тогда и только тогда, когда между членами этой пары имеет место отношение, сопоставленное с эмпирическом правилом смысла.

§ 6. Терминологические объяснения

Если некоторое предложение является 1) элементом области аксиоматического правила смысла или 2) элементом области дедуктивного правила либо элементом кообласти дедуктивного или эмпирического правила, или 3) элементом класса предложений, принадлежащего как элемент к области дедуктивного правила смысла, — тогда скажем, что соответствующее правило смысла охватывает это предложение.

Если какое-то выражение включено в предложение, охватываемое правилом смысла, то скажем, что это правило смысла относится к этому выражению. Правило смысла R для выражения А является несущественным тогда и только тогда, когда оно вообще не касается этого выражения, или же область этого правила смысла не изменится при замене во всех охватываемых правилом смысла предложениях выражения А произвольным выражением А’ того же логического типа, что и А, и vice versa. Если правило смысла для некоторого выражения, к которому оно относится, не является несущественным, тогда скажем, что это правило смысла для этого выражения существенно. Так, например, приведенное выше аксиоматическое правило смысла русского языка, позволяющее без оговорок признать каждое предложение вида “всякое А есть А”, является существенным как для выражения “всякое”, так и для выражения “есть”. Ведь если во всех предложениях вида “всякое А есть А” мы заменим выражение “есть” на “любит” (предположивши, что “любит” относится к тому же логическому типу, что “есть”), а также произведем замену “любит” на “есть” во всех возможных предложениях, то изменится область упомянутого правила смысла. Однако это же правило смысла несущественно для каждого имени, которое можно подставить вместо “А”. Очевидно, что если некоторое правило смысла несущественно для некоторого выражения А, то оно несущественно и для всех выражений, принадлежащих к тому же логическому типу, что А[6].

Если два выражения А и А’ одновременно входят в один и тот же элемент области правила смысла языка S, то скажем, что между А и А’ в языке S существует непосредственная смысловая связь. Если можно образовать конечную, состоящую по меньшей мере из трех членов последовательность выражений, первым членом которой является выражение А, последним же — В, и если между каждыми следующими друг за другом двумя членами этой последовательности существует непосредственная смысловая связь, то скажем, что между А и В существует опосредованная смысловая связь.

Коротко еще только отметим, что правила смысла языка касаются не только выражений, но также и синтаксических форм. Это отношение можно было бы определить подобно тому, как это было сделано для выражений. Далее, можно было бы отличать синтаксические формы, для которых правило смысла значимо, и такие, для которых незначимо. Наконец, подобно тому, как это было сделано выше, определить отношение смысловой связности между выражениями и синтаксическими формами. Но не будем на этом задерживаться.

§ 7. Определение правил смысла посредством смысла

Давайте сейчас займемся вопросом, должно ли изменение какого-то правила смысла языка приводить к изменению присущего языку подчинения выражениям их значений. Выше мы утверждали, что присущее языку подчинение смыслов однозначно определяет его правила смысла. Казалось бы, что это утверждение является ответом на поставленный выше вопрос. Однако нужно устранить некоторые недоразумения. А именно, мы не утверждаем, что присущее языку подчинение выражениям их смыслов определяет отдельные правила смысла; тем, что однозначно определено посредством этого подчинения, является в некотором смысле совокупностью правил смысла. Представим это четче. Как уже было сказано выше, каждому правилу смысла однозначно подчинена его область. Области отдельных правил смысла можно суммировать, если они принадлежат к одному логическому типу. Очевидно, что эти суммы могут остаться без изменения, хотя их составляющие, т. е. области отдельных правил смысла будут образованы различным образом. Говоря иначе, различные правила смысла могут иметь области, суммы которых идентичны. Утверждая, что присущее языку подчинение значений определяет правила смысла, мы хотели только то сказать, что это подчинение определяет сумму областей всех правил смысла.

Чтобы это пояснить на примере, допустим, что существует язык, в котором имеются только три, да и то аксиоматических правила смысла, первое из которых содержит предложение “2 x 2 = 4”, второе — предложение “1 + 1 = 2”, третье — предложение “1 x 1 = 1”. Сумма областей этих правил смысла — это класс, содержащий эти три предложения как элементы. Сейчас представим, что вместо этих трех правил смысла имеется только два, первое из которых содержит в своей области предложения “2 x 2 = 4” и “1 x 1 = 1”, а второе — только предложение “1 + 1 = 2”. Сумма областей этих двух правил такая же, как сумма областей ранее названных трех правил. Поэтому мы не утверждаем, что это изменение правил смысла влечет за собой изменение присущего языку подчинения смыслов, поскольку это изменение оставляет без изменений сумму областей этих правил.

В дальнейшем изложении для краткости будем называть совокупность сумм областей всех правил смысла “совокупной областью правил смысла”, хотя это не совсем правильно. Обратим внимание, что изменение совокупной области правил смысла может наступить двояким образом. Или же так, что в совокупную область войдут элементы, содержащие выражения, которые ранее не принадлежали языку, или без вхождения новых выражений в совокупную область. Говоря ранее, что изменение совокупной области правил смысла влечет за собой изменение смысла какого-то выражения, мы имели в виду только такие изменения, которые происходят без введения новых выражений. Прежде чем мы займемся вторым способом изменения совокупной области правил смысла и его влиянием на присущее языку подчинение смыслов, следует еще установить некоторое различие между языками.

§ 8. Языки замкнутые и открытые

Допустим, что существуют два языка S и S’, причем каждому слову и каждому выражению языка S соответствует одинаково звучащее выражение в языке S’, но не наоборот[7]. Кроме того, пусть одинаково звучащие выражения обоих языков будут взаимно переводимы. Теперь допустим, что некоторое выражение А’ более богатого языка S’, переводимое в А в языке S, является непосредственно связанным по смыслу с иным выражением А₁’, причем А₁’ не имеет перевода в язык S. В таком случае назовем язык S открытым языком относительно языка S’. Если мы захотим сказать, что некий язык является открытым относительно какого-то языка, то просто скажем, что язык является открытым. Если язык не является открытым, то назовем его замкнутым языком.

Мы выбираем термин “открытый язык” потому, что в таком языке можно увеличить запас выражений без изменения смысла выражений уже находящихся в нем. В частности, такой язык можно преобразовать в язык S’ посредством увеличения запаса его выражений, не изменяя смысла входящих в него выражений. Это не всегда возможно для замкнутого языка. В открытом языке определенные правила смысла как бы сокрыты в смысле выражений, поскольку выражение А уже в своем смысле так подогнано к смыслу еще отсутствующего в языке S перевода выражения А’, что когда этот перевод оказывается добавленным к запасу выражений языка S, выражение А вступит в соответствующие смысловые связи, не испытывая при этом изменений смысла. Но хотя эта подгонка к другому смыслу в некоторой степени уже подготовлена, она не проявляется при использовании языка вследствие его бедности. Обратная ситуация имеет место для замкнутых языков. В этих языках все особенности, содержащиеся в смысле их выражений, выходят на поверхность при использовании языка.

Сейчас мы можем заняться вопросом, поставленным в конце предыдущего параграфа, однако не решенным там. Должно ли изменение совокупной области правил смысла, заключающееся во введении новых выражений, приводить к изменению присущего языку подчинения смыслов? Этот вопрос для открытых и замкнутых языков мы должны рассмотреть отдельно. Начнем с языков замкнутых.

Допустим, что S является замкнутым языком; увеличивая запас его выражений некоторым выражением W, мы переходим к более богатому языку S_w. Язык S_w содержит все выражения языка S, а кроме них еще и выражение W. Совокупная область правил смысла языка S_w содержит кроме выражений языка S — назовем их старыми выражениями — еще выражение W. Сейчас речь идет о том, могут ли все старые выражения языка S_w иметь тот же смысл, который они имели в языке S. Здесь нужно отличать два аспекта. Или W находится в непосредственной смысловой связи со старыми выражениями языка S_w, или нет. Если да, то старые выражения в S_w не могут иметь тот же смысл, что в S, поскольку тогда S был бы открытым языком, или W имело бы смысл, тождественный смыслу одного из старых выражений, т. е. W имело бы перевод в одно из старых выражений. Из этого следует, что старые выражения в S_w только тогда могут иметь тот же смысл, что в S, когда или W не находится в непосредственной смысловой связи со старыми выражениями, или имеет тот же смысл, что и одно из них. Однако если выражение W не находится в непосредственной смысловой связи ни с одним старым выражением, то тем самым оно не находится ни в какой опосредованной смысловой связи.

Непустой частичный класс (nicht leere Teilklasse) выражений языка (вместо этого будем также говорить — “часть языка”), элементы которого не находятся ни в какой смысловой связи ни с одним выражением оставшейся части языка, будем называть изолированной частью этого языка. Если язык не обладает ни одной изолированной частью, тогда мы называем его связным языком (zusammenhangende Sprache). После этого из вышеизложенного можно сделать следующий вывод: если замкнутый язык S мы обогатим новым выражением W, не обладающим смыслом, равным смыслу какого-либо из старых выражений, и если старые выражения сохраняют в обогащенном языке S_w те же смыслы, которые они имели в языке S, то обогащенный язык S_w не является связным.

Сейчас обратимся к открытым языкам и спросим, должно ли изменить свой смысл выражение такого языка, если к этому языку присоединить новые выражения, т. е. если тем самым изменить совокупную область правил смысла этого языка? Из понятия открытого языка следует, что такой язык после присоединения новых выражений может сохранить смысл старых выражений и вместе с тем остаться языком связным, если после введения новых выражений он перейдет в язык, относительно которого он был открыт. При таком переходе возникает обогащенный язык, в котором совокупная область его правил смысла содержит как часть совокупную область правил смысла более бедного языка.

Сейчас, подытоживая, скажем: изменение совокупной области правил смысла языка посредством введения новых выражений в язык всегда влечет за собой изменение присущего языку подчинения смыслов настолько, что новое подчинение, кроме соответствий старых выражений их смыслам, содержит еще подчинение новых выражений их смыслам. Однако в подчинении смыслов старым выражениям только тогда не наступает никаких изменений, когда: 1) новый язык является несвязным или 2) вновь введенное выражение обладает таким же смыслом, как и одно из старых выражений, или 3) старый язык является открытым относительно языка нового.

Если язык S посредством присоединения одного или более выражений переходит в язык S’, относительно которого он был открыт, то мы говорим, что язык S оказался дополненным до замыкания языка S’. В противном случае мы говорим: язык S’ оказался низведенным до открытого языка S. Если язык S дополняется до замыкания языка S’, а язык S’ сам является языком замкнутым, то мы говорим: язык S оказался полностью дополненным до замыкания языка S’.

Можно ли дополнить открытый язык S до замыкания различных связных языков? Конечно, это возможно, если язык не будет полностью замкнут уже посредством добавления одного выражения. А именно, добавляя к открытому языку S выражение W, или выражение V, или оба вместе, и дополняя его частично до замыкания языка S_w, или S_v, или S_w,_v и т. д. до тех пор, покамест посредством добавления все новых выражений мы не придем к полностью замкнутому языку. Является ли этот путь единственным, которым можно дополнить открытый язык до связного замкнутого языка? Если да, то для открытого языка существовал бы один единственный замкнутый и связный язык, до которого его можно было бы дополнить. Это привело бы к совершенно парадоксальным последствиям. В частности, по следующей причине: допустим, что открытый язык S удается полностью дополнить до замкнутого языка S’ посредством добавления нескольких выражений, среди которых выражения W₁ и W₂. Пусть языку S’ будет присуще следующее подчинение смыслов: выражению W₁ соответствует смысл δ₁, выражению W₂ — смысл δ₂. Рассмотрим другой язык S’’, в той единственной подробности отличающийся от языка S’, что в S’’ выражению W₁ подчинен смысл δ₂, тогда как выражению W₂ — смысл δ₁. Очевидно, что дополнение открытого языка S до замыкания языка S’’ точно так же возможно, как и его дополнение до замыкания языка S’. Если бы так не произошло, то это значило бы, что в открытом языка, например, в языке обычного исчисления предложений с первичными терминами “Й“ и “~“, но без определяемых знаков, можно ввести знак “v“ или знак “•“, с обычно приписываемыми им смыслами, но нельзя ввести эти знаки со взаимно изменяемыми смыслами. Это следствие не может быть принято, поскольку оно совершенно противоречит тому, что вообще понимается под смыслом. Учитывая сказанное, можно дополнить полностью открытый язык до замыкания двух различных связных языков.

Сейчас мы исследуем, в каком отношении должны находится два различных замкнутых и связных языка S’ и S’’, если существует открытый язык S, который можно полностью дополнить до замыкания равно как языка S’, так и S’’. В исследованном выше случае S’’ возник из S’ вследствие обмена смыслов выражений W₁ и W₂. Следовательно, там мы занимались двумя взаимно переводимыми языками. Мы называем S’ переводом языка S’’, если все выражения одного языка могут быть взаимно однозначно подчинены выражениям другого таким образом, что взаимно подчиненные друг другу выражения имеют один и тот же смысл. Сейчас перед нами возникает вопрос, обязательно ли должны быть взаимно переводимыми два замкнутых и связных языка S’ и S’’, если можно полностью дополнить до их замыкания открытый язык S?

Чтобы ответить на этот вопрос, мы должны несколько ближе заняться понятием перевода.

§ 9. Синонимы и переводы

Сначала мы установим условие равноосмысленности (Sinngleichheit) или синонимичности двух выражений А и А’ одного и того же языка S. Оно звучит так: если А и А’ обладают в языке S одним и тем же смыслом, то их поведение единообразно в совокупной области правил смысла языка, т. е. совокупная область правил смысла не должна претерпеть изменения вследствие того, что во всех ее элементах произойдет подстановка А’ вместо А, и А вместо А’. Это значит: 1) если согласно какому-то правилу смысла предложение Z должно быть безоговорочно признано, то существует аксиоматическое правило смысла, согласно которому следует безоговорочно признать предложение, полученное из предложения Z посредством замены А’ на А и А на А’; 2) если существует дедуктивное правило смысла, согласно которому можно из предложения (или из класса предложений) Z₁ вывести предложение Z₂, то существует также дедуктивное правило смысла, согласно которому из предложения, возникшего из Z₁ посредством замены А’ на А и А на А’ можно вывести предложение, возникшее из Z₂ посредством замены А’ на А и А на А’; 3) если согласно эмпирическому правилу смысла на основании определенных данных можно признать предложение Z, то существует также правило смысла, согласно которому на основании этих же данных следует признать предложение, возникшее из предложения Z посредством замены А’ на А и А на А’.

Заметим здесь, что равноосмысленность и эквивалентность двух выражений — это не одно и то же. Два выражения А и А’ эквивалентны, если каждому истинному предложению, содержащему А, соответствует истинное предложение, возникшее из него посредством замены А’ на А и А на А’, и наоборот. Два эквивалентные в приведенном здесь понимании выражения вовсе не должны быть равноосмысленны. Так, например, в логическом исчислении предложений Уайтхеда и Рассела выражения “a Й b” и “~ a v b” эквивалентны, но не равноосмысленны, поскольку, например, существует дедуктивное правило смысла, требующее готовности вывода “b” на основании “a Й b” и “а”, тогда как аналогичного правила смысла для “~ a v b” нет. Из приведенной выше дефиниции эквивалентности можно через абстракцию получить дефиницию [логической] валентности выражения, которая в случае, например, имен дает дефиницию области имени (в терминологии Милля — денотации).

Приведенное выше необходимое условие равноосмысленности двух выражений одного и того же языка влечет за собой некоторые следствия, которые мы не хотим обойти молчанием. А именно, речь идет о том, являются ли два выражения А и В, считающиеся по определению равными, имеющими также один и тот же смысл. Ответ зависит от того, как понимается дефиниция. Если дефиниция является правилом вывода, которое, например, говорит, что, если какое-то предложение признается и можно также признать предложение, полученное из него вследствие замены А на В, и наоборот, то выражения А и В не обязаны обладать одним и тем же смыслом. Это как минимум следует из установленного выше необходимого условия равноосмысленности двух выражений одного и того же языка.

Допустим, что в языке имеется аксиоматическое правило смысла, содержащее в своей области предложение “F [a]”, но нет аксиоматического правила смысла, которое бы в своей области содержало “F [b]”. Пусть, кроме этого, обязательно дедуктивное правило смысла, основывающееся на дефиниции, которая объясненным выше образом признает равными знаки “а” и “b”. Очевидно, что поскольку правила смысла языка опосредованно или непосредственно ведут к признанию некоторого предложения “F [a]”, то они приводят также к признанию “F [b]”, согласно приведенному выше (основанному на дефиниции “а = b”) правилу смысла, поскольку согласно этому правилу смысла везде правомерной будет замена “а” на “b”. Однако несмотря на это “а” и “b” не выполняют выше установленного условия равноосмысленности. Правда, существует аксиоматическое правило смысла, требующее безоговорочной готовности признания “F [a]” (как аксиомы), но нет такого, которое требовало бы безусловного признания “F [b]” (как аксиомы), хотя “F [b]” дедуктивно следует из “F [a]” и как следствие аксиомы “F [a]” является утверждением.

Совершенно иным будет ответ на вопрос, выполняют ли необходимое условие для равноосмысленности два приравненных дефиницией выражения, когда такого вида дефиниция будет понята не как правило вывода, а как утверждение о правилах вывода и аксиомах. Если мы понимаем дефиницию, устанавливающую равенство выражений “А” и “В” как утверждение, провозглашающее: “каждое правило вывода должно (с этого момента) говорить о “В” то же, что и о “А”, и каждой аксиоме “F [A]”, выполняемой “А”, соответствует предложение “F [B]”, выполняемое “В”, которое также является аксиомой, то уравненные так понимаемой дефиницией выражения “А” и “В” выполняют также необходимое условие равноосмысленности (по крайней мере в дискурсивных языках). Кажется, что по крайней мере в дедуктивных системах дефиниции никогда не понимаются иначе, т. е. как утверждения о правилах смысла и аксиомах, но всегда считаются или правилами смысла, или (что встречается реже) теоремами системы. Таким образом, установленное нами необходимое условие равноосмысленности не выполняется двумя выражениями, уравненными дефиницией дедуктивной системы. Мы отмечаем это следствие, которое, возможно, кто-нибудь захочет понять как instantia contraria против высказанного нами в тексте утверждения. Подвергнутое сомнению условие не составит большого труда преобразовать таким образом, чтобы освободиться от выше приведенного следствия. Для этого нужно было бы трактовать приведенное условие как единственную альтернативу так, что ему противопоставлялась в качестве второй альтернативы равенство по определению.

Сейчас обратимся к вопросу равноосмысленности двух выражений, принадлежащих разным языкам. Если выражение А обладает в языке S тем же смыслом, что и выражение А’ в языке S’, то назовем выражение А переводом А’ из языка S’ в язык S. Отношение перевода является рефлексивным, симметричным и транзитивным отношением. Допустим, что какое-то выражение А’ является переводом выражения А из языка S в язык S’. Пусть выражение А в языке S находится в разнообразных непосредственных смысловых связях с прочими выражениями А₁, А₂, …,А_n определенных синтаксических форм и, возможно, также с некоторыми чувственно воспринимаемыми данными. Как кажется, формулируемое следующим образом утверждение полностью соответствует повсеместно принятому понятию перевода: “если выражение А’ является переводом выражения А из языка S в язык S’, и если А в языке S находится в непосредственных смысловых связях с А₁, А₂, …, А_n, и выражения А₁, А₂, …,А_n также переводимы в язык S’ (обозначаемые соответственно А’₁, А’₂, …,А’_n), то А’ также должно находится в S’ в аналогичных непосредственных смысловых связях с А’₁, А’₂, …,А’_n как А с выражениями А₁, А_2, …,А_n в языке S. Таким образом, если, например, аксиоматическое правило смысла безоговорочно предписывает признать предложение, построенное из выражения А и прочих выражений А₁, А₂ в соответствии с синтаксической формой К, и если А’ должно быть переводом А, то поскольку имеются также переводы А₁ и А₂ (обозначаемые А’₁ и А’₂), а также перевод синтаксической формы (обозначаемой К’), то для языка S’ должно быть обязательным правило смысла, согласно которому следует безоговорочно признать построенное из А’, А’₁, А’₂ предложение в соответствии с синтаксической формой К’. Допустимые в языке синтаксические формы составных выражений определены синтаксическими правилами языка и присущи языкам так же, как и их запас слов, а поэтому подлежат переводу, как и слова[8].

Подобно аксиоматическим оставшимся правилам смысла языка также должны соответствовать аналогичные правила смысла в другом языке, если выражения одного языка, к которому относятся эти правила смысла, должны быть переводимы на другой язык. Прежде чем мы это утверждение сформулируем точнее, отметим следующее. Ранее мы установили условие переводимости А в выражение А’ из языка S в S’ с тем, что если А находится в непосредственной смысловой связи с А₁, А₂, …,А_n, то и А’ находилось бы в аналогичных смысловых связях с переводами выражений А₁, А₂, …,А_n из языка S в S’, если такие переводы существуют. Сужение этого утверждения замечанием “если переводы выражений А₁, А₂, …,А_n в язык S’ существуют” только тогда необходимо, когда мы не ограничиваемся замкнутыми языками, но принимаем во внимание также открытые языки, поскольку из дефиниции замкнутого языка S’ непосредственно следует, что в случае существования в нем перевода выражения А из языка S, существуют в нем также переводы всех тех выражений, с которыми А находится в S в непосредственных смысловых связях. Таким образом, если речь идет о замкнутых языках, то упоминавшееся ограничение установленного выше утверждения можно опустить.

Ранее мы говорили, что если выражение А в языке S находится в непосредственных смысловых связях с некоторыми выражениями А₁, А₂, …,А_n, то перевод А из языка S в S’ должен находится в аналогичных смысловых связях с переводами выражений А₁, А₂, …, А_n. Поскольку смысловые связи отображаются в областях правил смысла, а следовательно, также в их совокупной области, постольку мы можем — ограничиваясь замкнутыми языками — придать упоминаемому утверждению следующую формулировку: если А’ является переводом А из языка S в S’, а также S и S’ суть языки замкнутые, то все элементы совокупной области правил смысла языка S’, содержащие А’, должны быть образованы из элементов совокупной области правил смысла языка S, содержащих А, таким образом, что в области, названной последней, заменится везде А на А’, а остальные, содержащиеся в них выражения (и синтаксические формы) — их переводами[9].

Сейчас мы займемся языками взаимно переводимыми и взаимно непереводимыми. Мы всегда будем иметь в виду дословные переводы, т. е. переводы выражения в выражение, а не только предложение в предложение. Два языка назовем взаимно переводимыми тогда и только тогда, когда каждому выражению одного языка соответствует одно или несколько выражений другого языка, являющиеся его переводами с одного языка на другой, и vice versa.

Мы утверждаем следующее: если два языка S и S’ являются оба замкнутыми и связными, и если в языке S’ имеется выражение А’, являющееся переводом выражения А из языка S в S’, то оба языка взаимно переводимы. Если бы было иначе, то в S существовало бы выражение А_n, которому в языке S’ не соответствовал бы ни один перевод, или vice versa. Однако, если определенное выражение замкнутого языка непереводимо на другой замкнутый язык, то и все непосредственно связанные с ним по смыслу выражения должны быть непереводимыми. Пусть, например, А_x будет выражением непосредственно связанным по смыслу с А_n. Если А_n из языка S непереводимо на S’, то и А_x должно быть непереводимо, ибо если бы А_x имело свой перевод в S’, то и непосредственно связанные по смыслу с А_x выражения, а среди них А_n, должны были бы иметь свои переводы в S’ (поскольку согласно предположению S’ является замкнутым языком). Однако А_n, как мы предположили, не переводимо. По этой же причине не будут переводимы всяческие возможные А_y, непосредственно связанные по смыслу с А_x. Далее, можно было бы доказать, что выражения, непосредственно связанные по смыслу с непереводимыми А_y, опять же непереводимы и т. д. Однако все эти выражения являются одно — либо многоступенчато опосредованно связанными по смыслу с А_n. Таким образом, если А_n непереводимо, то все непосредственно и опосредованно связанные по смыслу с А_n выражения непереводимы.

Сейчас примем во внимание класс выражений языка S, связанных по смыслу с А_n (обозначим его S₁), и класс оставшихся выражений языка S (обозначим его S₂). Первый класс состоит исключительно из непереводимых выражений, а поэтому не содержит выражение А, поскольку оно, вследствие допущения, переводимо. Таким образом, класс S₂ не пуст. Ни одно из принадлежащих ему выражений не может находится в смысловой связи с каким-либо выражением из класса S₁, поскольку оно тогда вступило бы в связь по смыслу с А_n и принадлежало бы S₁. Итак, если выражение А переводимо, тогда как А_n — нет, то отсюда следует, что класс выражений языка S можно разделить на два непустых класса, причем между выражениями обоих классов не возникают никакие смысловые связи, т. е. язык S не является связным. Однако это противоречит предположению, которое мы сделали относительно языка S.

Тем самым мы доказали, что если S и S’ являются языками связными и замкнутыми и некоторое выражение одного языка переводимо в другой язык, тогда все выражения этого языка переводимы на другой.

Сейчас мы можем вернуться к вопросу, может ли открытый язык быть дополнен до замыкания двух замкнутых и связных, взаимно непереводимых языков? На основании сказанного выше ясно, что так быть не может. Если бы так было, то существовало бы два замкнутых и связных языка, в которых некоторые выражения были бы переводимы (а именно, выражения, общие с открытым языком), другие же нет. Это противоречит только что доказанному утверждению.

Из выше приведенных рассуждений следует, что каждый смысл, который мы находим в замкнутом и связном языке, можно обнаружить и в каждом языке, который с данным языком взаимно переводим, однако кроме этого [языка, упомянутый смысл] не находится ни в одном другом замкнутом и связном языке. Система всех находящихся в замкнутом и связном языке смыслов не пересекается ни с одной другой такой системой. Такую систему смыслов назовем понятийным аппаратом (Begriffsapparatur). Нельзя пользоваться ни одним языком, в который одновременно входят смыслы из двух различных понятийных аппаратов без того, чтобы перейти тем самым к несвязному языку.

§ 10. Попытка определения “смысла”

До настоящего времени мы в рассуждениях поступали таким образом, что, не вводя дефиниции термина “смысл” и опираясь на общепринятое его понимание, выводили некоторые относящиеся к смыслу утверждения, из которых в дальнейшей последовательности рассуждений выводили последующие заключения на основании безапелляционных дефиниций нескольких технических терминов. Сейчас мы предложим дефиницию термина “смысл”, на основании которой все выше высказанные утверждения удастся четко обосновать. Эту дефиницию мы не будем “доказывать”, т. е. показывать ее согласованность с общепринятым понятием смысла, ибо “общепринятое понятие смысла” является весьма изменчивым понятием. Именно по этой причине невозможно совпадение четко разграничивающей дефиниции с такого вида понятием. Поскольку мы стремимся к четко очерченному понятию, то для нас вовсе не желательно, чтобы наша дефиниция полностью соответствовала обыденному понятию смысла. Тем не менее мы хотели бы, чтобы у читателя сложилось впечатление, что установленная нами дефиниция, по крайней мере, в своем объеме соответствовала бы существеннейшей из всевозможных интенций, скрывающейся под именем “смысл”. Добавим также, что предлагаемую дефиницию мы едва очертим, не претендуя на полноту и совершенство. И еще одно замечание: говоря в дальнейшем изложении о языках, мы будем принимать во внимание только языки замкнутые и связные, поскольку ранее названные открытые языки являются собственно фрагментами языков замкнутых, которые единственно и заслуживают называться полным языком. Несвязные языки также не являются языками в собственном смысле, но произвольными отпечатками немногих связных языков.

Сейчас мы начнем очерчивать нашу дефиницию. Языком мы называем образование, однозначно определенное классом знаков и матрицей (Matrix), образованной из этих знаков, а также, возможно, чувственных данных (матрице соответствует ранее обсуждавшаяся совокупная область правил смысла). Элементы этого класса знаков, совместно очерчивающие язык, мы назовем выражениями языка. Матрица языка — это таблица, составленная из трех частей, одна из которых соответствует сумме областей всех аксиоматических правил смысла, вторая — сумме областей всех дедуктивных правил смысла, а третья — сумме областей всех эмпирических правил смысла. Первая часть состоит из строк, каждая из которых является последовательностью. Отдельные члены этой последовательности образованы из всех выражений, входящих в некоторую аксиому этого языка (т. е. в предложение, принадлежащее к области аксиоматического правила смысла), в том числе и из самой аксиомы. Принцип упорядочивания, согласно которому эти выражения следуют друг за другом в строках, зависит от синтаксической роли выражений в предложении и является одним и тем же во всех строках. Этот принцип можно сформулировать так: сначала всё выражение, потом его главный функтор, затем первый аргумент этого функтора, затем второй аргумент и т. д. Согласно этому принципу упорядоченные выражения, входящие в конъюнкцию предложений, например, “Иван любит Марию и Иосиф любит Анну” образовывали бы следующую последовательность: 1) “Иван любит Марию и Иосиф любит Анну”, 2) “и”, 3) “Иван любит Марию”, 4) “любит”, 5)”Иван”, 6)“Марию” 7) “Иосиф любит Анну”, 8) “любит”, 9) “Иосиф”, 10) “Анну”. Или, например, символы предложения “p v q . є . ~ p Й q” согласно этому принципу были бы упорядочены так:

1) “p v q . є . ~ p Й q”, 2) “є“, 3) “p v q”, 4) “v“, 5) “p”, 6) “q”, 7) “~ p Й q”, 8) “Й“, 9) “~ p”, 10) “~“, 11) “p”, 12) ”q”

Вторая часть матрицы, соответствующая дедуктивным правилам смысла, состоит из строк, каждая из которых является упорядоченной парой последовательностей. Вместе с тем, эти последовательности определены на области, или же соответственно кообласти, дедуктивных правил смысла так же, как строки, образующие первую часть нашей матрицы, определены на области аксиоматических правил смысла.

Третья часть матрицы состоит из пар, каждая из которых содержит в качестве первого члена данное опыта, тогда как в качестве второго — последовательность выражений предложения (а также само предложение), подчиненного этому данному опыта посредством эмпирического правила смысла.

Привести пример матрицы фактически существующего языка было бы чрезвычайно трудно. Однако мы изобразим язык, в котором существует небольшое количество выражений (допустим, одиннадцать), обозначенных первыми одиннадцатью литерами алфавита. Ограничим количество данных опыта, существенных для этого языка, до трех и обозначим их a, b , γ. Тогда матрица этого языка могла бы иметь такой вид:

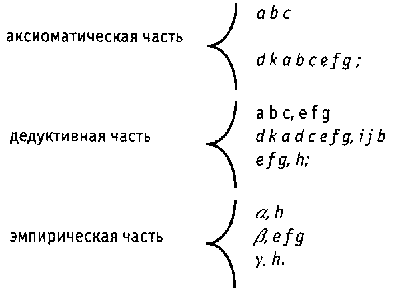
Из этой таблицы видно, что в этом языке имеется только пять предложений, а именно — a, d, e, h, i; при этом предложение а содержит выражения b, c; предложение e — выражения f, g; h является предложением, образованным из одного слова, d является предложением, соединяющим предложение а с предложением е при помощи функтора k; наконец предложение i содержит выражения j и b.

Из этой матрицы также видно, что 1) аксиоматические правила смысла содержат в своей области два предложения, в частности а и d, т. е. нужно быть готовым признать эти два предложения, невзирая на обстоятельства, если нет намерения нарушать подчинения смыслов, присущих этому языку; 2) дедуктивные правила смысла требуют готовности выведения предложения e из предложения а, предложения i из предложения d и предложения h из предложения e, если не должно быть нарушено присущее языку подчинение смыслов; и наконец 3) эмпирические правила смысла требуют готовности признать предложение h равно как относительно данных опыта a, так и γ, а также признания предложения е относительно данных опыта b, если имеющиеся в языке смыслы не должны быть нарушены.

Сейчас мы устанавливаем дефиницию переводимости двух языков, причем для упрощения не будем принимать во внимание такие языки, в которых имеются синонимы. Дефиницию, принимающую во внимание такие языки, мы приведем ниже мелким шрифтом.

Языки S и S’ являются взаимно переводимыми посредством отношения R тогда и только тогда, когда R есть одно-однозначное отношение, которое каждому выражению S ставит в соответствие выражение S’, и наоборот таким образом, что матрица S (или же S’) переходит в матрицу S’ (или же S), если в ней заменить все выражения выражениями, подчиненными им посредством R.

Два выражения языка мы называем синонимами, когда они являются изотопами в матрице языка, т. е. когда матрица [с точностью] до порядка строк остается неизменной, если мы совершим взаимный обмен обоих этих выражений.

Дефиниция переводимости, принимающая во внимание также и языки, содержащие синонимы, звучала бы так: S и S’ взаимно переводимы с учетом R тогда и только тогда, когда 1) S и S’ суть языки и классы всех их выражений можно поделить на два подкласса так, что выражения из первого подкласса ни в коем случае не являются между собой синонимами, а каждое выражение второго подкласса (который может оказаться пустым классом) является синонимом какого-то выражения первого подкласса; 2) R является одно-однозначным отношением, которое каждому выражению первого подкласса языка S ставит в соответствие выражение первого подкласса языка S’ таким образом, что если в матрице языка S (или же S’) заменить каждое принадлежащее области отношения R выражение языка S (или же S’) выражением языка S’ (или же S), сопоставленное ему R, то получится матрица, которая отличается от матрицы языка S’ (или же S) не более, чем изотопными выражениями. Мы говорим, что матрица отличается от другой матрицы не более чем изотопными элементами, если обе матрицы можно преобразовать в одну матрицу следующей операцией: выбираем в каждом классе взаимно изотопных элементов один из них, положим а, и вычеркиваем в матрице все строки, содержащие изотопный с а элемент, но оставляем не зачеркнутыми те строки, которые содержат а, но не содержат ни одного изотопного с а элемента.

Сейчас мы приводим дефиницию: А в языке S обладает тем же смыслом, что А’ в языке S’ тогда и только тогда, когда А является выражением языка S, А’ — выражением языка S’ и существует отношение R, с учетом которого S переводимо в S’ и А находится в отношении R к А’.

Определенное выше отношение равноосмысленности является отношением равенства, т. е. рефлексивным, симметричным и транзитивным; следовательно, на основе этого отношения можно определить смысл как семейство классов (свойств) абстракции по отношению равноосмысленности. На основании этой дефиниции можно сказать: смысл А в языке S — это то свойство А в языке S, которое присуще некоторому А’ в языке S’ тогда и только тогда, когда А’ в S’ равноосмысленно с А в S.

Поскольку можно взаимно отобразить матрицы всех взаимно переводимых языков, то можно сказать, что все такие матрицы изоморфны, или же что они имеют одну и ту же структуру. С целью более выразительного представления структуры матрицы обозначим последовательности выражений, находящиеся в строках матрицы, номерами, и сделаем это следующим образом: последовательности, входящие в строки первой (аксиоматической) части обозначим арабскими цифрами, начиная с “1”. Последовательности, находящиеся в строках второй (дедуктивной) части, также обозначим, начиная с “1”, арабскими цифрами, но последовательность, находящуюся в этой строке на первом месте, получит эту цифру с одним штрихом (например, 2’), тогда как последовательность, находящаяся на втором месте, получит эту же цифру с двумя штрихами (например, 2’’). Последовательности выражений, находящиеся в третьей (эмпирической) части обозначим римскими цифрами, опять же начиная с “I”. Находящееся в начале строки данное опыта получит эту же римскую цифру с добавлением с правой стороны нуля, отделенного от римской цифры запятой (например, пусть “II,0”).

Кроме того, пусть выражения каждой последовательности будут одно за другим пронумерованы (независимо от оставшихся последовательностей) арабскими цифрами, начиная с “1”. Для однозначной характеризации места, занимаемого каким-либо выражением в нашей матрице, достаточно привести номер соответствующей последовательности (содержащей это выражение), а также номер, соответствующий этому выражению в последовательности. Таким образом, каждая позиция в матрице однозначно определена парой номеров. Если, например, мы хотим привести все позиции, которые занимает выражение е в выше приведенной матрице, то делаем это при помощи следующих пар номеров:

(2, 6) (1’’, 1) (2’, 6) (3’, 1) (II, 1).

С этого момента эти пары номеров будем называть позициями матрицы. Допустим, что мы кого-то проинформировали, как это сделано выше, о смысле этих пар номеров. Проинформируем еще, какие позиции нужно заполнить одинаково звучащими выражениями. Это можно сделать следующим образом: поделим все позиции матрицы на классы так, что позиции, принадлежащие одному классу, должны быть заполнены одним и тем же образом, тогда как две позиции, принадлежащие разным классам, должны быть заполнены различным образом. Во-вторых, скажем еще, какими опытными данными следует заполнять позиции типа: “римская цифра, ноль”. Проинформированный таким образом человек сможет запроектировать различные матрицы, которые однако будут между собой разниться не более, чем словесным звучанием отдельных выражений и которые можно будет взаимно свести друг к другу посредством соответствующего одно-однозначного словарного отношения. На основании приведенной информации можно запроектировать матрицу всех языков, переводимых на данный язык. Такая информация содержала бы всё и только то, что обще матрицам всех языков, переводимых на данный язык, но умалчивала бы исключительно их индивидуальные свойства.

То, что обще всем таким матрицам, мы назовем их структурой. Что содержит наша информация? Мы привели класс позиций, которые должны быть заполнены одинаково звучащими выражениями и подчиненность некоторых данных опыта позициям типа “римская цифра, ноль”. Итак, можно сказать: “совокупность[10] (Zusammenfassung) всех классов позиций выражений, которые должны быть заполнены одинаково звучащими выражениями (короче: классы равных позиций), и соответствий между данными опыта и позициями типа “римская цифра, ноль” — это структура матрицы. Смыслом А в S мы назвали то свойство, которое имеет А в S общим со всеми равноосмысленными А’ в S’ и только с ними. Из того, что сказано выше ясно, что это свойство заключается в занятии в матрице с данной структурой одной из тех позиций, которые принадлежат к данному классу равных позиций. Данный смысл однозначно определен заданием класса равенств позиций и структурой матрицы. Можно было склоняться к высказыванию, что смысл — это пара “класс равенств (Gleichklasse), структура”. Если приведена структура матрицы, то тем самым однозначно очерчен класс всех пар “класс равенств, структура”, а тем самым — класс всех смыслов, присущих выражениям языка с этой структурой. Но [âåðíО] также и обратное.

Выше мы ввели термин “понятийный аппарат”, понимая под этим класс всех смыслов, принадлежащих выражениям замкнутого и связного языка. Относительно того, что сказано выше, можно сформулировать следующее: структура матрицы и понятийный аппарат взаимно определимы.

Сейчас напрашивается вопрос, который мог бы кто-нибудь задать в отношении матрицы, если ему действительно предъявили бы все классы позиций выражений, которые следует соответствующим образом заполнить, но вместо соответствий между местами типа “римская цифра, ноль” и данными опыта предъявить только классы позиций типа “римская цифра, ноль”, которые следует заполнить таким же образом. Матрицы, которые могли бы быть образованы на основе этих данных, отличались бы не только словесным звучанием выражений, но могли бы на одних и тех же местах типа “римская цифра, ноль” содержать иные опытные данные. Тогда это не были бы матрицы взаимно переводимых языков. Однако все эти языки отличались бы между собой не более, чем эмпирическими правилами смысла, тогда как в дискурсивных правилах смысла (так были названы, как уже упоминалось, все неэмпирические правила смысла) они были бы согласованы. Класс всех классов, к которым принадлежат позиции выражений, которые должны быть единообразно заполнены, т. е. класс классов равенств будем называть дискурсивной структурой языка. В отличие от этого класс всех классов позиций типа “римская цифра, ноль”, которые должны быть одним и тем же образом заполнены, мы назовем эмпирической структурой языка.

В языках сугубо математических систем (например, геометрии) их структура покрывается (deckt sich) дискурсивной структурой, поскольку для них не обязательны никакие эмпирические правила смысла. Каждый язык, обладающий эмпирической структурой, но в своей дискурсивной структуре, согласованный со структурой математической системы, образует эмпирическую интерпретацию языка этой системы.

§ 11. Обыденное понятие “языка”

Многие из наших утверждений, на которых основаны наши рассуждения, читатель может посчитать ложными, если под “языком” будет понимать то, что имеется в виду, когда говорят о “языке немецком”, “языке французском”, “языке польском” и т. д. Возьмем одно из первых утверждений, которое говорит, что двое людей не пользуются одним и тем же языком потому, что с одними и теми же выражениями они связывают различный смысл. Допустим, что две личности, пользуясь языком, не нарушают ни русской фонетики, ни синтаксиса, но один из них под “звездой” понимает только постоянные звезды, второй — также планеты, тогда как прочими выражениями они пользуются в одном и том же смысле. Разве мы скажем, что один из них говорит по-русски, а второй не говорит по-русски? Мне кажется, что нет! Если две личности пользуются одними и теми же выражениями, но связывают с ними различные смыслы, то мы скажем о них, что они не говорят на одном и том же языке лишь тогда, когда эти расхождения достаточно значительны. Если смыслы, которые они связывают с выражениями, хотя несколько и разнятся, однако весьма подобны, тогда мы скажем про обоих, что они говорят на одном языке, если выражение “язык” мы будем понимать обыденным образом.

Из этого следует, что обыденное понимание “языка” изменчиво в той же степени, что и понятие “достаточно значительного подобия”. Поэтому для таких семасиологических рассуждений, какие мы проводим, обыденное понятие “языка” так же неупотребительно, как понятия “горячий” и “холодный” для физики, или “большой” и “малый” для математики. То понятие языка, которое мы имели в виду, в качестве образца использует понятие обыденного языка таким же образом, как, например, понятие “воды” в химии использует понятие “воды” в обыденной жизни.

Мы понимаем язык так, что для его однозначной характеристики не достаточно более или менее установленного соответствия между словом и смыслом, но требуется совершенно точное соответствие смыслов. Придерживаясь этого точного понятия языка, мы не сможем сказать, что существует один русский язык, но должны утверждать, что существует много русских языков, звучащих одинаково, но отличающихся — хотя не очень значительно — соответствием слов и смыслов. Фактически можно насчитать несколько русских языков (опуская различные диалекты и исторические фазы); существует несколько одинаково звучащих естественных русских языков, существует русский язык физики, русский язык медицины и т. д. О том, что в обычном смысле слова язык не является единственным языком (в нашем смысле), но в точном смысле множественностью (Mehrheit) языков, забывают теоретики познания, и это неоднократно приводило к пагубным последствиям. Согласно нашей терминологии, в соответствии с которой для однозначного определения языка необходимо однозначное подчинение выражениям их смыслов, ни в одном языке нет двузначного выражения. Одно-единственное двузначное выражение указывает на существование двух одинаково звучащих языков, отличающихся только одним — соответствием между выражениями и смыслами.

Если мы не забудем о различии между нашей трактовкой термина “язык” и тем, что обычно понимается под этим термином, то, возможно, исчезнут предостережения относительно утверждения, что в каждом языке имеются однозначно очерченные определенные правила смысла. Поскольку для “языка” (здесь выражение взято в обычном смысле) соответствие смыслов установлено не точно, то и правила смысла, в которых проявляется это соответствие, не являются однозначно очерченными. В понятых таким образом языках правила смысла так же изменчивы, как и соответствие смыслов. Не встречаем мы этого там, где соответствие значений точно определено, например, в языках сугубо дедуктивных систем, в первую очередь, в языках символической логики. Правила смысла для этих языков можно легко привести на основании аксиоматики и правил вывода. Таким образом, язык логической системы является в точном значении этого слова языком, хотя языком почти всегда открытым.

Перевод с немецкого Бориса Домбровского

[1] Sprache und Sinn. “Erkenntnis” IV, 1934, S. 100-138.

[2] Das Weltbild und die Begriffsapparatur. “Erkenntnis” IV,1934,S. 259-287.

[3] E. Husserl. Logische Untersuchungen. Halle, Niemeyer, 1913. II. Bd., I. Teil, Unt. I: Ausdruck und Bedeutung.

[4] Я пробовал дать такую дефиницию в статье “О смысле выражений” (O znaczeniu wyrazen),- Lwów 1931. Księga pamiątkowa Polskiego Towarzystwa Filozoficznego we Lwowie.

[5] Недавно Р. Карнап обратил внимание на связь между смыслом выражения и критериями для предложений, в которое входит это выражение. См. “Ueberwindung der Metaphysik durch logische Analyse der Sprache”. Erkenntnis, Bd. 2,H. 4, S. 221. В месте цитирования Карнап ссылается на аналогичные взгляды в Tractatus logico-philosophcus (1922) Виттгенштейна, который должен был сказать: “Смысл предложения заключается в его критерии истинности”. Я допускаю, что этот “критерий истинности” родственен нашим правилам смысла.

[6] Допустим, что Z есть предложение языка S, в котором для Z нет реально значимого правила смысла. Является ли такое предложение разрешимым в принципе? Предложение языка назовем разрешимым в принципе, если оно или положительно, или отрицательно разрешимо. Скажем, что предложение языка разрешимо в принципе положительно, если это предложение принадлежит объему аксиоматического правила смысла или принадлежит как элемент к кообласти эмпирического правила смысла, или же образует второй член в паре, принадлежащей как элемент объема дедуктивного правила смысла, и в этой паре первый член состоит только из предложений, разрешимых в принципе положительно (кажущегося порочного круга в этом определении можно избежать, превратив его в определение-цепь (Ketten-Definition). Если отрицание предложения является положительно разрешимым в принципе, то назовем предложение отрицательно разрешимым в принципе. Если бы предложение Z, для которого ни одно правило смысла данного языка не является значимым, было бы однако разрешимо в принципе, то каждое предложение этого языка должно было бы быть или положительно, или отрицательно разрешимо в принципе в зависимости от того, является ли Z положительно или отрицательно разрешимо. Так должно быть потому, что все правила смысла, относящиеся к этому предложению, были бы тогда для него несущественны и тем самым говорили бы о нем то же, что и о всех прочих предложениях. Языки с отрицанием, в которых все предложения разрешимы однонаправлено, являются противоречивыми языками. Если мы проигнорируем языки, в которых все предложения разрешимы однонаправлено, то должны сказать, что предложения, для которых ни одно правило смысла не является значимым, должны быть неразрешимы в принципе. Однако обращение этого утверждения не верно, поскольку для некоторого предложения может не быть, например, значимо ни аксиоматическое, ни эмпирическое правило смысла, но дедуктивное, которое трактует это предложение только в своей области и иначе, чем все прочие предложения. Такое предложение было бы в принципе неразрешимо, хотя определенное правило смысла является для него значимым. Если предложение, для которого ни одно правило смысла не значимо, мы назовем предложением, лишенным смысла (выражение мы называем бессмысленным, если к нему вообще не применимо ни одно правило смысла; в этом случае оно не принадлежит языку), то мы вынуждены сказать, что каждое предложение, лишенное смысла, неразрешимо в принципе, но не каждое неразрешимое в принципе предложение лишено смысла.

Разрешимости в принципе противопоставляется фактическая разрешимость. Эту всегда следует — по нашему мнению — релятивизировать к определенной области опытных данных. Дефиниция фактически разрешимого предложения с учетом области G опытных данных звучала бы аналогично дефиниции в принципе разрешимого предложения; единственно вместо альтернативы “предложение принадлежит к кообласти эмпирического правила смысла” нужно было бы сказать:” предложение образует второй член пары, принадлежащей к области эмпирического правила смысла и содержащей в качестве первого члена данные опыта области G”.

[7] С этого момента под “выражением” будем также понимать отдельные слова, а не только составное выражение.

[8] Существуют логические языки исчисления предложений, в которых некоторые их функции высказывания пишутся таким образом, что в середине находится знак функции, слева от него — ее первый аргумент, справа — ее второй аргумент (например, “pЙp”). Существуют также другие логические языки, которым такой способ построения чужд и в которых, в отличие [от упомянутых], имеются высказывательные функции, когда сначала пишется знак функции, следующий первым, а затем второй аргумент (например, в нотации Лукасевича “Cpq” — см. Jan Lukasiewicz. Philosophische Bemerkungen zu mehrwertigen Systemen des Aussagenkalkul. Warszawa 1930, ”Comptes rendus des seances de la Societe des Sciences et de Lettres de Varsovie”, Classe III.). Один способ построения является переводом второго и тогда “p F q” есть перевод “F p q”.

[9] В настоящем исследовании мы понимаем “перевод” как перевод совершенный или дословный. Однако можно говорить также о несовершенном переводе, например, тогда, когда можно перевести все предложение, исключая возможность перевода отдельных образующих его слов. Чтобы учесть это понятие, мы должны были бы несколько либерально сформулировать установленное выше условие того, что выражение было бы переводом иного выражения, уже не требуя, чтобы все, относящиеся к этому единственному выражению в языке S смысловые связи, отражались бы в языке, на который мы это выражение переводим, но ограничивая это требование до нескольких смысловых связей, которые тогда нужно будет определить точнее. Однако заняться этой темой подробнее мы здесь не можем.

[10] Мы выбираем точно не определенный термин “совокупность” вместо “класс”, поскольку соответствие (т. е. упорядоченная пара) не принадлежит к тому логическому типу, что класс и поэтому нет класса, который содержал бы в качестве элементов классы и соответствия. Вместо “совокупность” мы могли бы говорить об упорядоченной паре, т. е. об отношении, область которого имела бы один элемент, а именно — класс всех классов позиций выражений, которые должны быть таким же образом заполнены, а кообласть в качестве единственного элемента содержала бы класс всех выше названных соответствий.

[ предыдущая статья ] [ к содержанию ] [ следующая статья ]